Oversampling, the wrong way
Posted on April 26, 2023. Tags: machine learning, data science, classificationSome mistakes are sillier than others, and I just caught myself making one of the sillier ones. I thought I’d share my experience and hopefully save someone else the embarrassment :).
Some background for the uninitiated
Recently, I was tasked with training a model for a multiclass text classification task. If that jargon doesn’t make sense to you, imagine this: you have a giant stack of papers in front of you, and you want to sort these papers into 4 (or 2, or 10) different piles (called “classes”) depending on what’s written on them. Your stack of papers might be thousands or even millions of papers tall, so it’s just not viable to manually sit there and sort them out yourself; instead, you decide to use ✨ machine learning magic ✨ to do it for you.
The machine learning model can’t just read your brain and do your bidding; you need to tell it what you want it to do, and this is generally achieved by showing it some examples that you have manually labeled yourself. For instance, you may show it that this paper should belong in Pile 1, while that paper should get put in Pile 2. This process is called training, and the hope is that after showing it some number of examples, it’ll be able to guess where the papers should go with a decent level of accuracy.
How do we decide how accurate it is? We need to test the model, that is, give it some new papers that it’s never seen before (but that we do know the correct labels for) and see if it guesses those labels correctly. Generally, we just receive a ton of examples and their labels in one huge file, and we split the data up ourselves into training and testing data. We train the model on the training set, showing it examples and their correct labels, and then we evaluate its performance on the testing set, where we give it examples and check if its guess matches the correct label. This is called the train-test split.
It doesn’t make sense to test the model on data it was trained on, because that’s cheating; the model already saw what the label is meant to be, so chances are it’ll be an easy slam dunk when you ask it again. Testing models on training data leads to artificially inflated accuracy scores that provide no insight on how well the model generalizes to real-world data. Keep this in mind for later.
Training tribulations
Earlier, why did I say “hope” instead of “guaranteed result”? Well, training is known to be a rather finicky process. Models often come with all kinds of different knobs and dials that you can turn (with fancy names such as “weight decay” or “gamma”), slight tweaks of which can cause your model to either learn successfully or crash and burn and perform at no better than random guessing.
And sometimes, if your training examples are imbalanced, it may skew the model one way or another. Suppose you showed the model 100 examples of papers which should go in Pile 1, but only 5 examples of papers which should go in Pile 2. This might lead the model to conclude that Pile 2 papers are just much rarer than Pile 1 papers (whether or not that’s true in the real world), and so it becomes far more likely to guess 1 than 2 when faced with a new paper.
I was faced with this issue in my own task. Below is the class distribution of pre-labeled examples I was given:
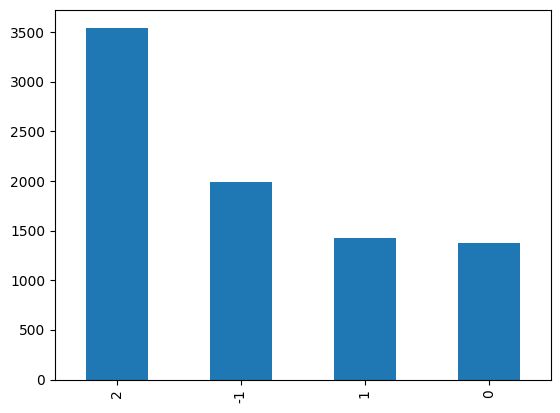 The x-axis are my different classes, and the y-axis is the number of training
examples in a given class
The x-axis are my different classes, and the y-axis is the number of training
examples in a given class
As you can see, I have more than double the number of examples labeled “2” than I do examples labeled “0”, even though this is certainly not the case in the real world (in reality, I would guess that “0” would probably show up a lot more often than “2”).
How do we combat this? One strategy is undersampling, in which we just throw out examples from the overrepresented class(es) until we have roughly equal numbers of examples in each class. This can be great, if you’re a massive corporation like Google with roughly unlimited data, but my measly few thousand examples are precious, and I need all that I can get to train my model.
So, the opposite approach (called – you guessed it – oversampling) is to randomly make copies of examples in the underrepresented classes, in order to bring up the total number of examples in each of those classes to match the overrepresented class. This doesn’t add anything “new” per se, but it causes the examples in the underrepresented class to be, in a sense, weighted more.
The mistake
So it seems like we’re good to go! I can just use oversampling to resolve the class imbalance issue in my data, and I’m all set. I can then split my data into a training and testing set, and start training my model on the training set and testing on the testing set, right?
Right?
Did you catch it? I didn’t. Remember when I said it’s important to make sure you’re testing your model with examples it’s never seen before? When we oversample, we duplicate examples in our data. If we then split our duplicate-containing data into train and test sets, it’s almost definitely going to be the case that some examples will show up in both the training and the testing sets.
As a result, the accuracy looked really good; in reality, it was just super inflated because we were testing it on examples it had already seen during training. Fixing this mistake brought my accuracy score down by a robust 15%. Don’t do this, and avoid having to tell your team that unfortunately you are not a ML whisperer, but in fact a rather normal individual.
What should you do instead? Train-test split first, then oversample your training data.