Emergent fractals

Let’s play a game.

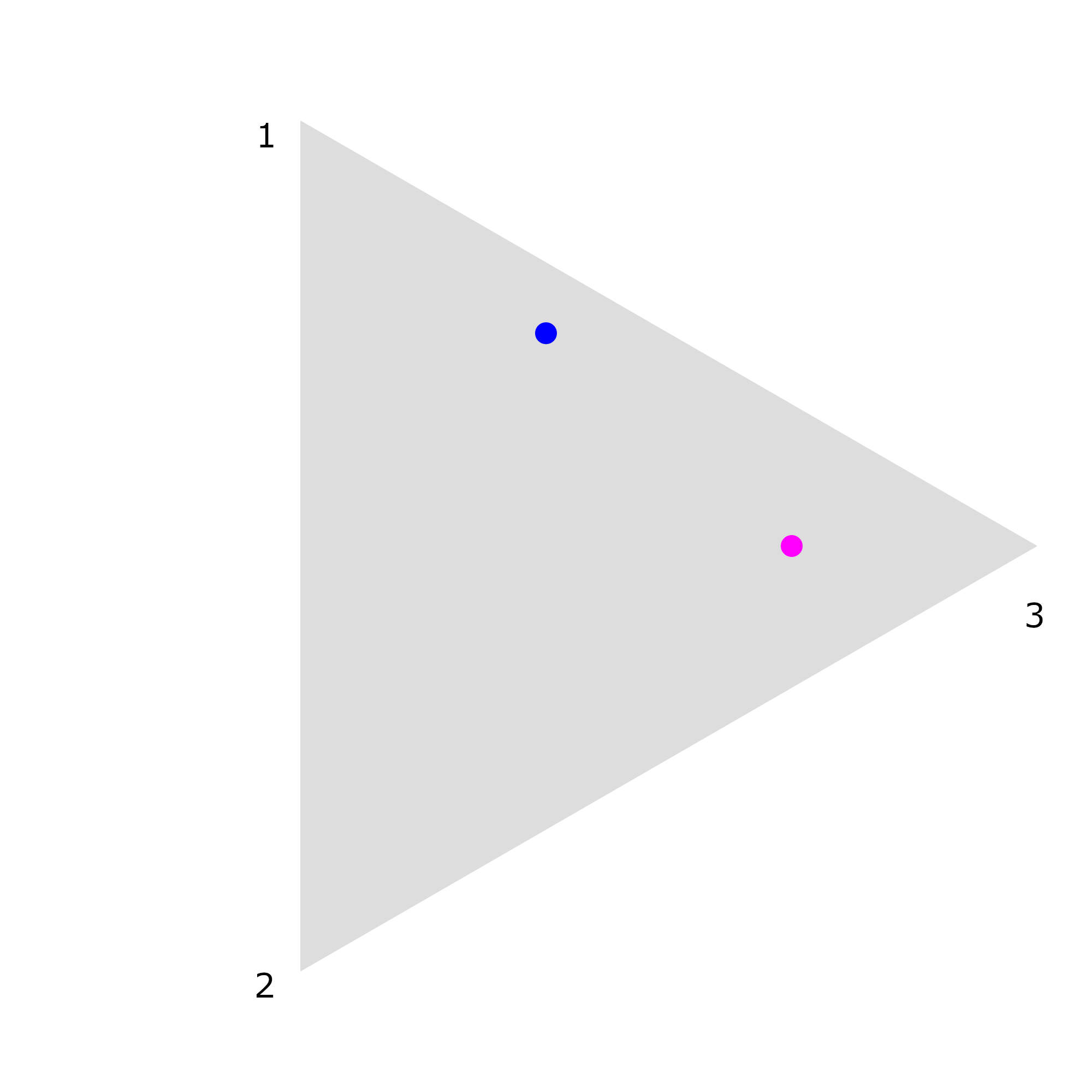
Our game board is a triangle, with corners labeled 1, 2, and 3. Our piece is a small stamp, which can start at any random spot in the board, but we’ll just put it in the middle for demonstration purposes.

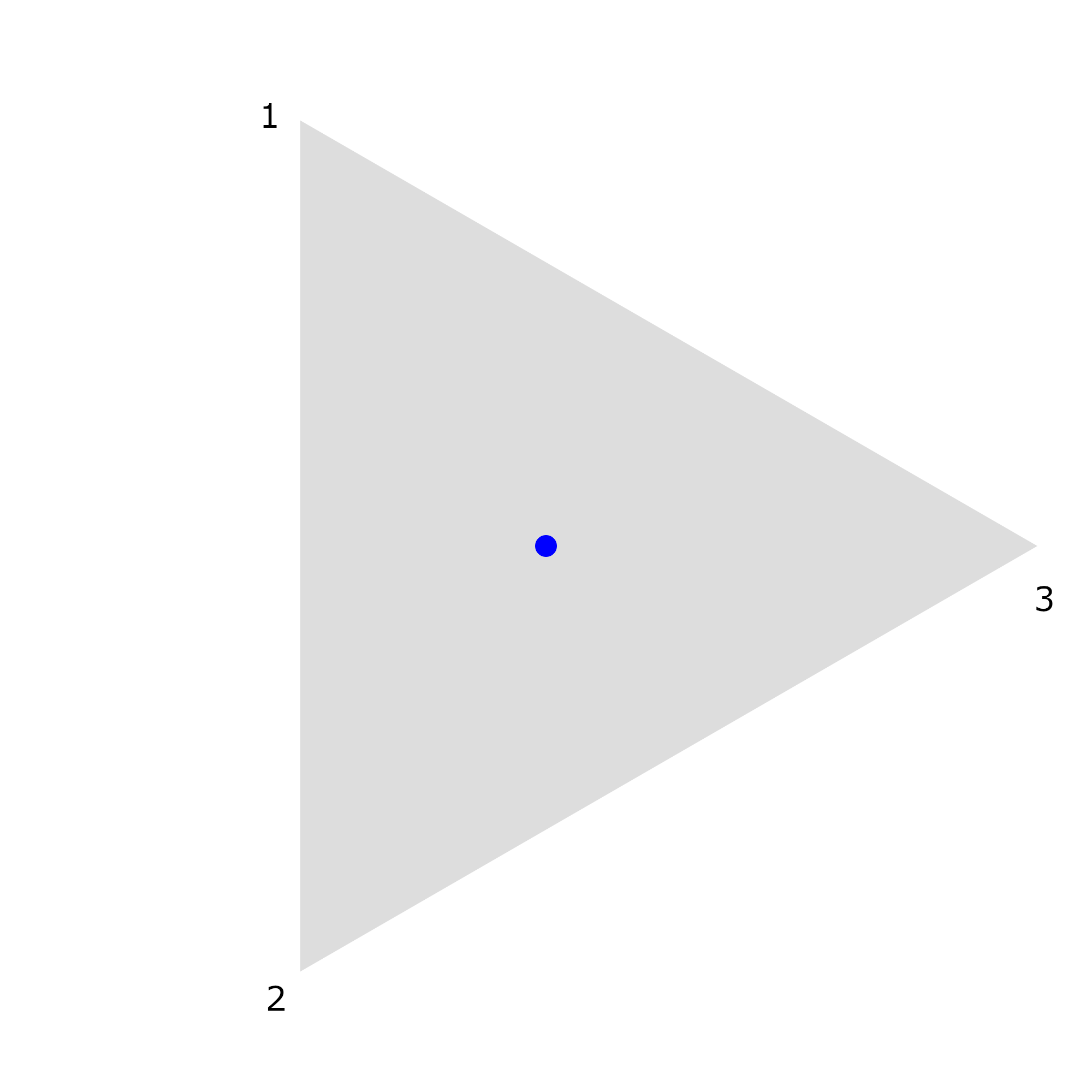
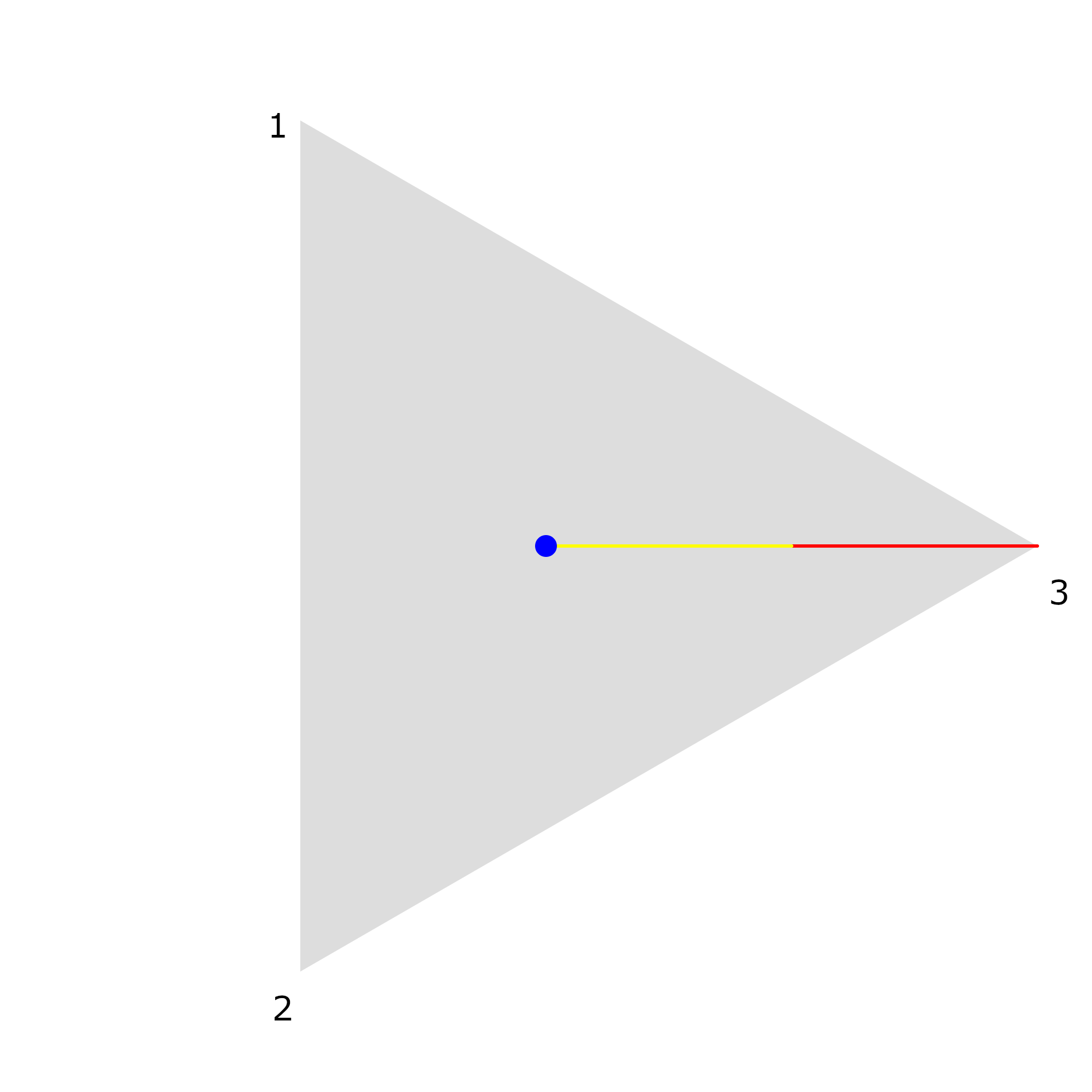
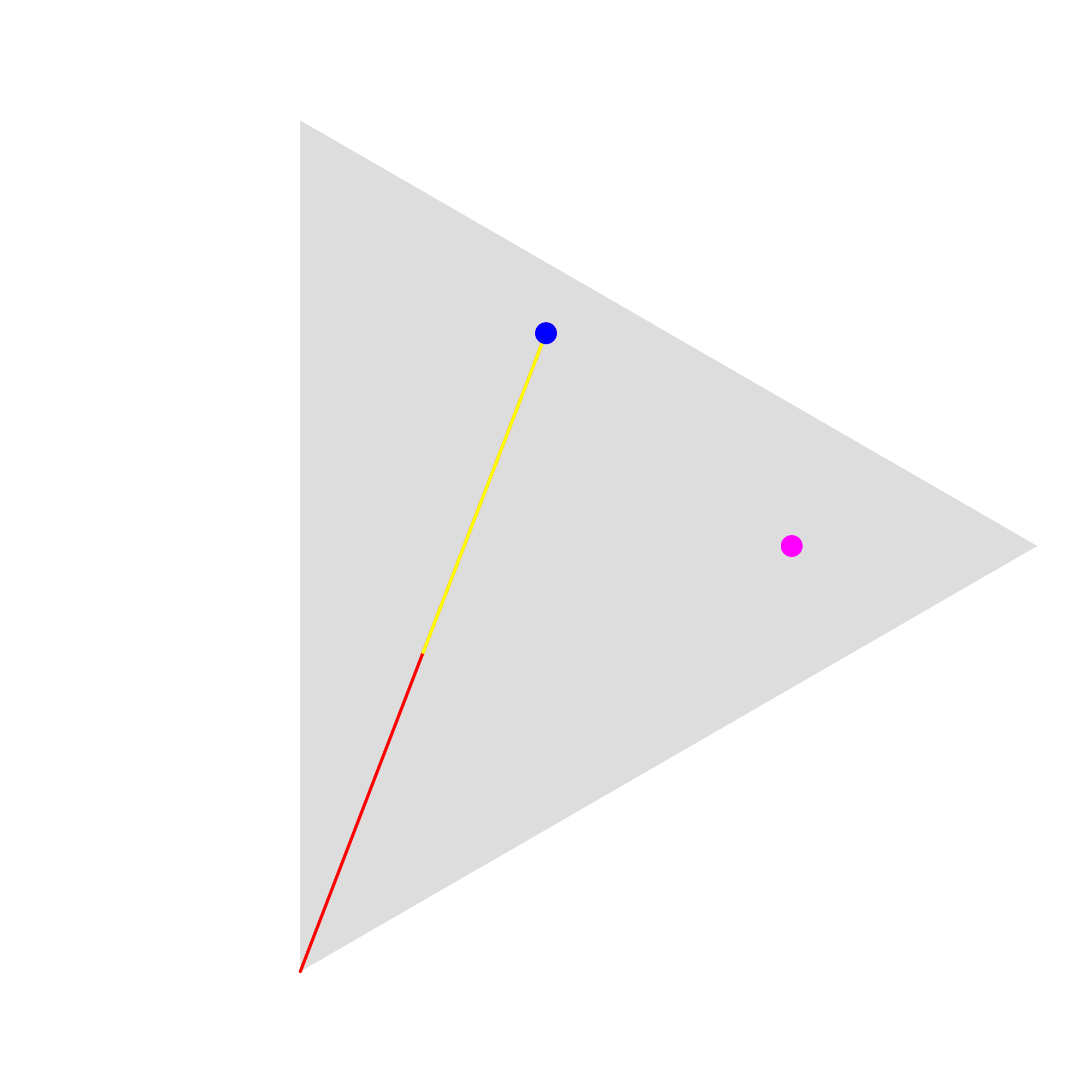
Every turn, we roll a three-sided dice; based on the number that ends facing up, we move our stamp half of the way towards that corner, and make a stamp mark. For example, let’s say we rolled a 3. Then we’ll be moving towards the rightmost corner of the triangle, along the red line; we only move halfway, so we’ll be moving right to where that yellow line ends.

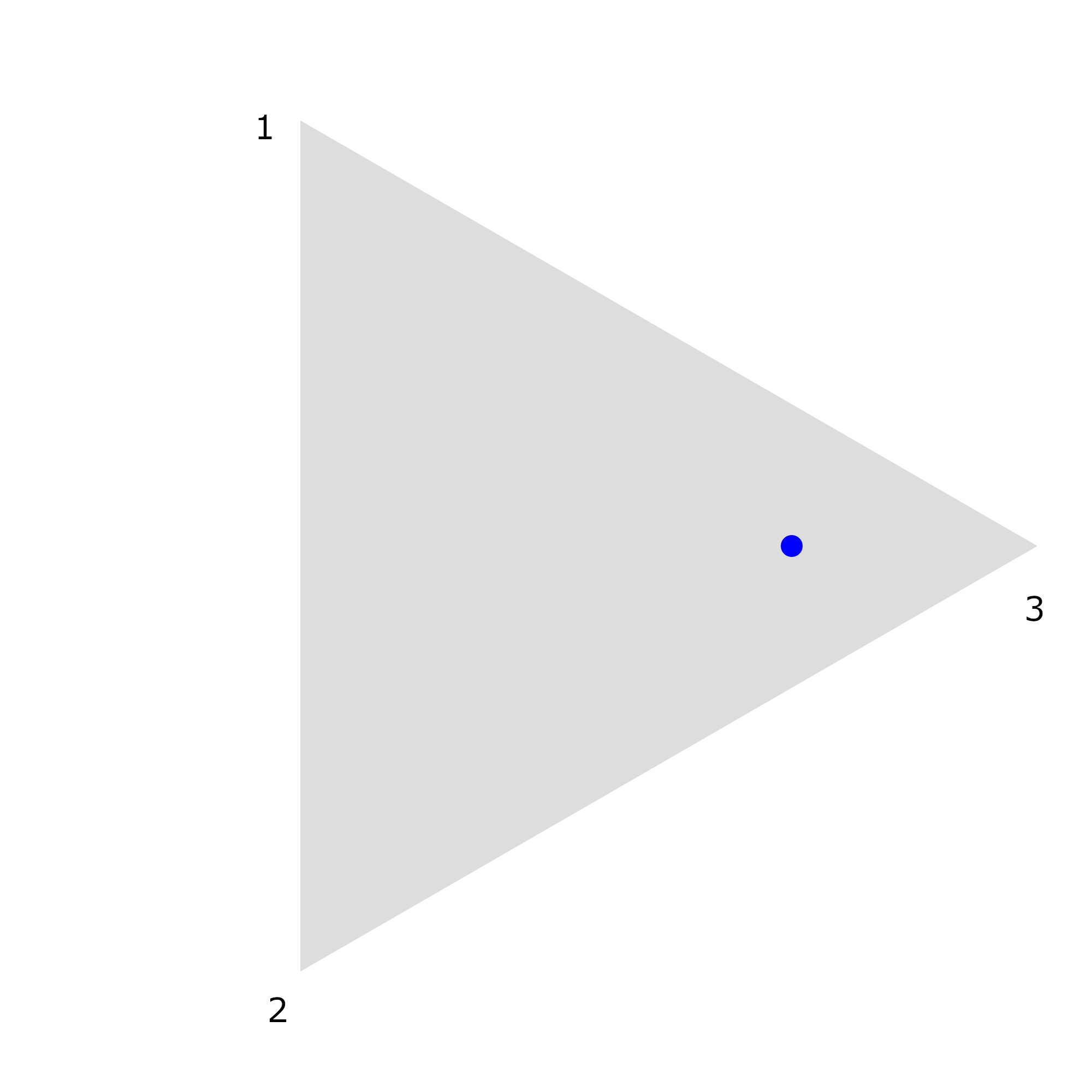Moved the stamp. We make a mark with the stamp when we move it.

Let’s do it again! This time we rolled a 1 with the dice, so we’re heading up to the topmost vertex.

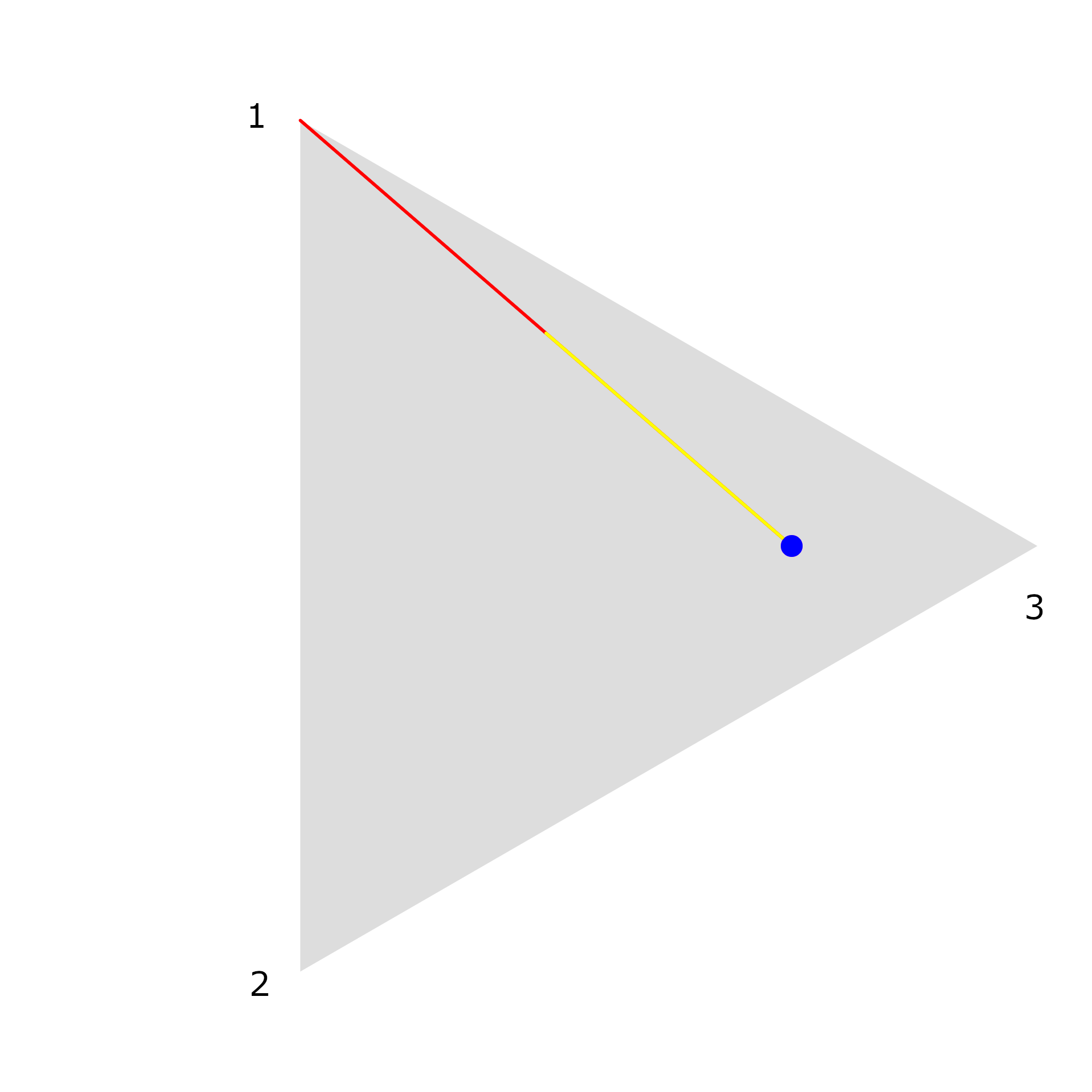
Notice the stamp mark we left behind at our previous spot.

And we can continue still further…

I think you get the point by now, so let’s speed it up and see what happens after we play a few thousand rounds of this game.

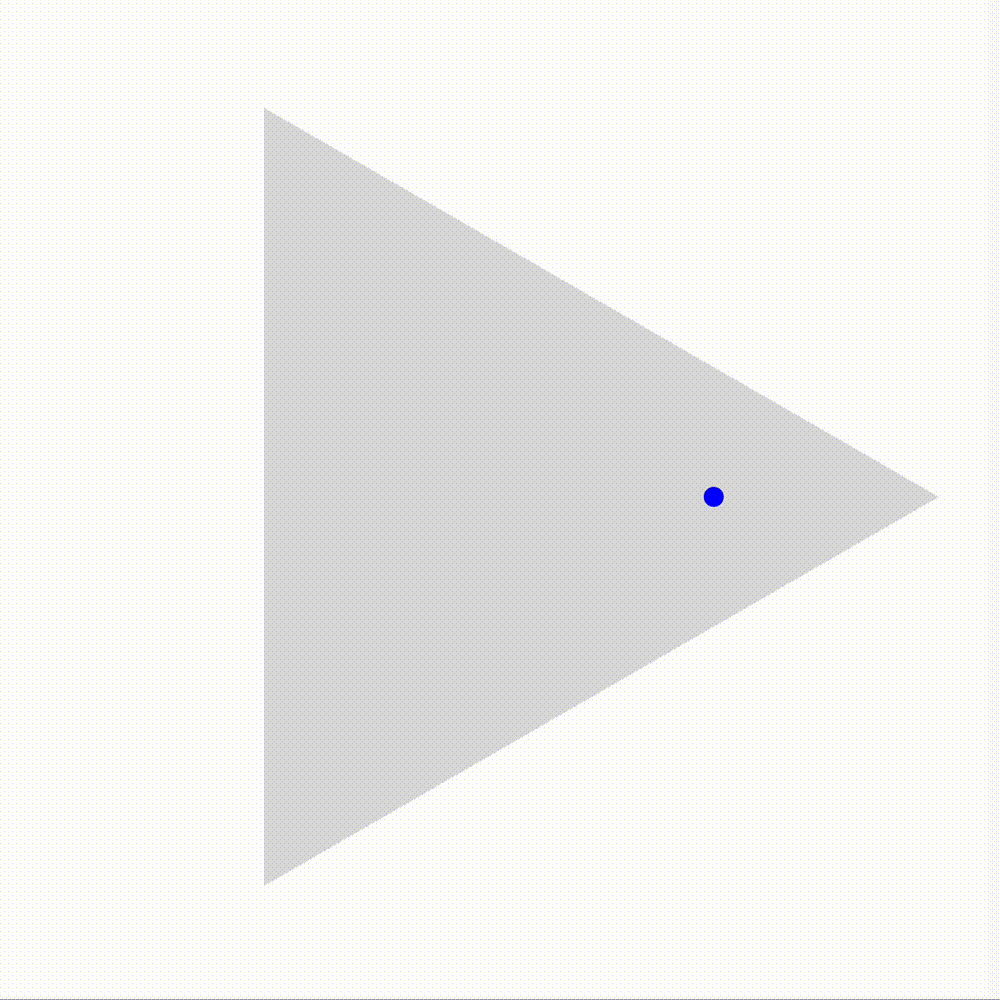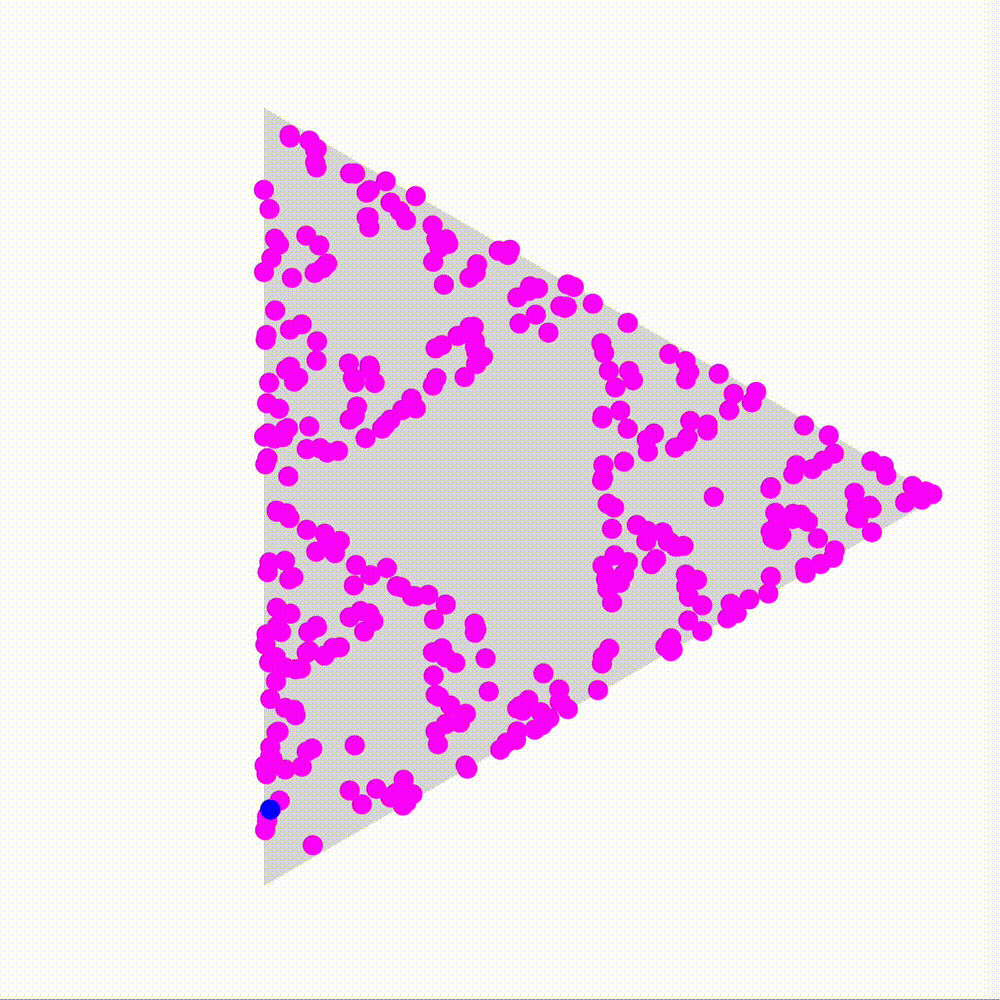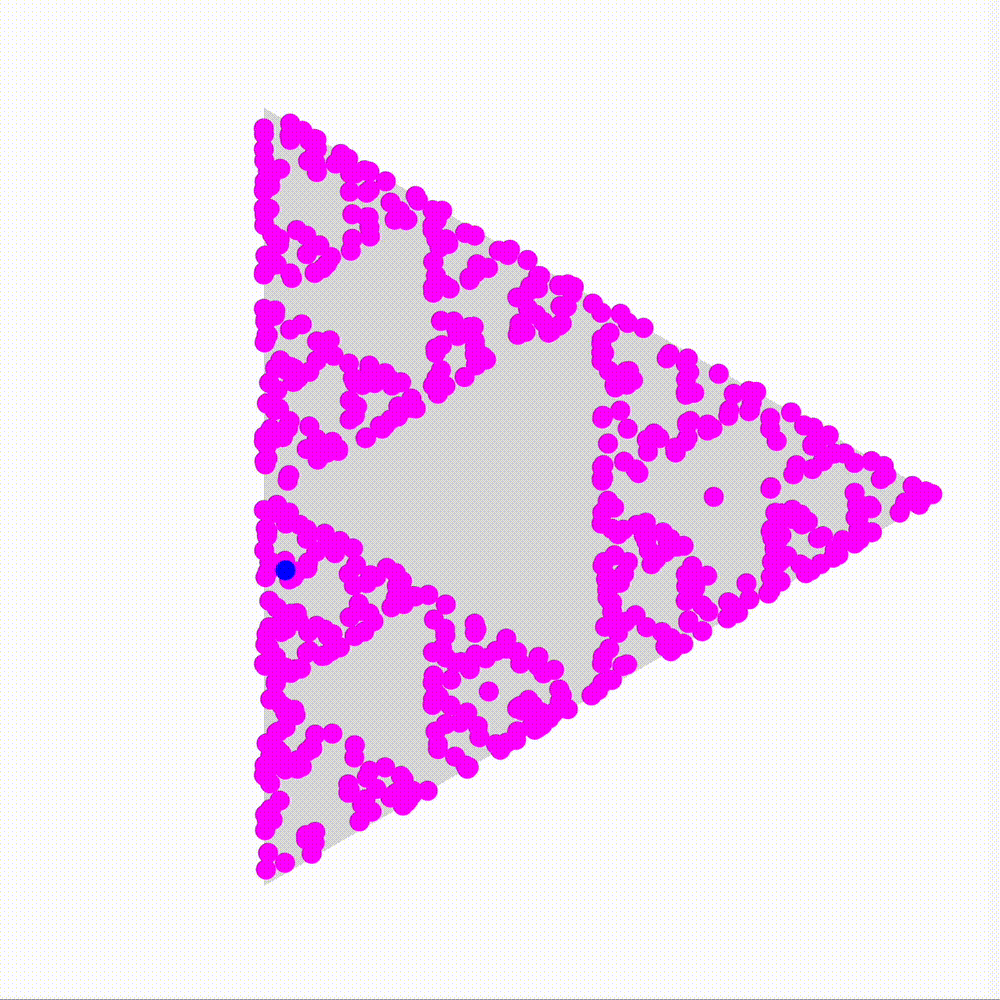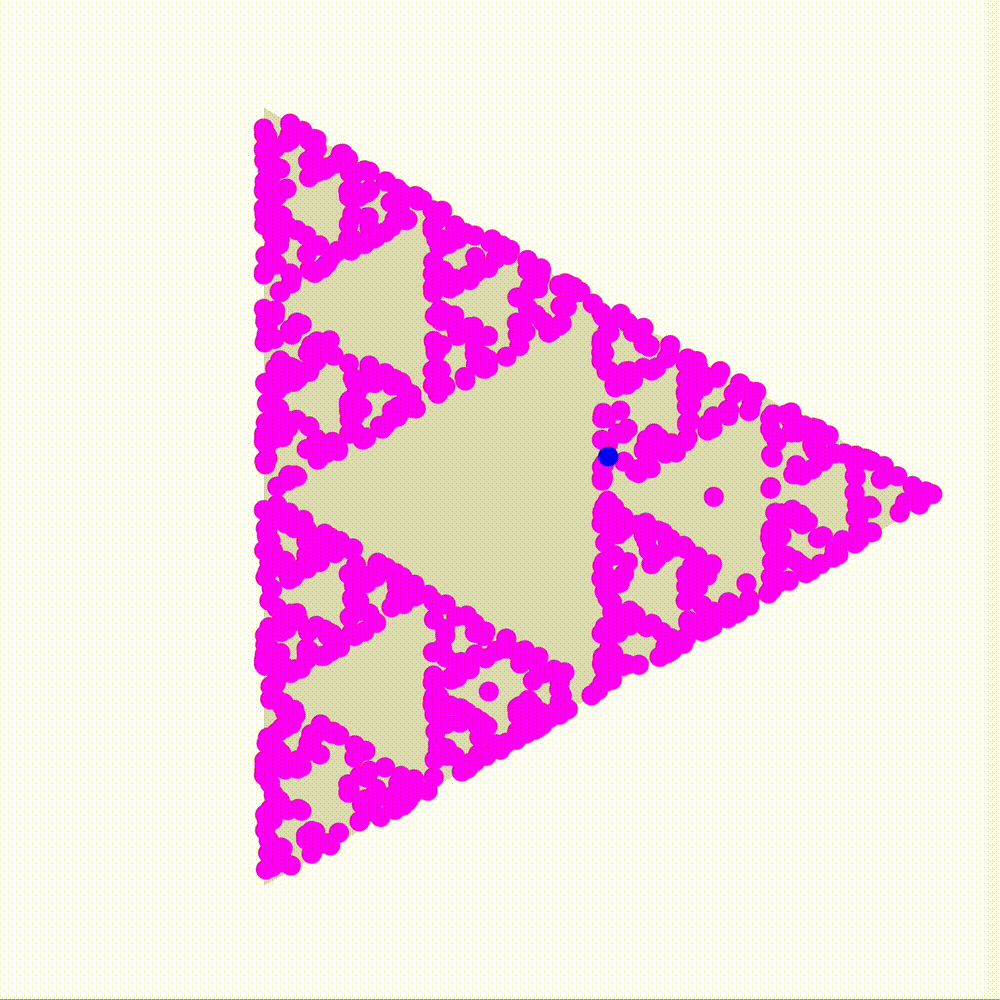
Huh, that’s weird.

What I’ve described is a phenomenon known as the Chaos game, in which a fractal emerges from this repeated random process. There’s a lot of different variations to be explored; for example:

• What if we used another shape that’s not a triangle? Will we still get fractals with squares, pentagons, and n-gons in general?
• What if we jumped a different distance than one-half?
• What if instead of heading directly at the vertex we rolled with a dice, we headed in that direction, but with some offset / rotation?
• What if we limited our choice of vertices? For example, what if we disallow jumping towards the same vertex twice, or if we disallow choosing neighboring vertices?

That’s a lot of variables to explore, so I put together a quick p5.js sketch to play around with it. Instead of using big, clunky circles, I’ve instead just had it draw a tiny point, so it’s easier to see what’s going on. The coloring of the point is determined by the magnitude of the distance that we jumped from the previous step, i.e. bluer dots are further jumps.

let loc;
let NUM_VERTICES = 5;
let STEP_RATIO = 50/100;
let COLOR1, COLOR2;
let TWIST = 0.0;
let vertices = [];
let ALLOW_SAME_VERT = true;
let ALLOW_NEIGHBOR_VERT = true;
let prev_vert = 0;

function setup() {
  createCanvas(1000, 1000);
  loc = createVector(0, 0);
  COLOR1 = color("#00467F");
  COLOR2 = color("#A5CC82");
  for (let i = 0; i < NUM_VERTICES; i++) {
    let v = p5.Vector.fromAngle(i / NUM_VERTICES * TWO_PI);
    v.mult(width * 0.45);
    vertices.push(v);
  }
}

function draw() {
  translate(width / 2, height / 2);
  for(let i = 0; i < 10000; i++) {
    let target = 0;
    while(true) {
      target = floor(random(NUM_VERTICES));
      if (!ALLOW_SAME_VERT && target == prev_vert) continue;
      if (!ALLOW_NEIGHBOR_VERT && 
          ((target + 1) % NUM_VERTICES == prev_vert ||
           (prev_vert + 1) % NUM_VERTICES == target))
        continue;
      break;
    }
    prev_vert = target;
    let diff = p5.Vector.sub(vertices[target], loc);
    stroke(lerpColor(COLOR1, COLOR2, diff.mag() / (width * 0.9)));
    diff.mult(STEP_RATIO);
    diff.rotate(TWIST);
    loc.add(diff);
    point(loc.x, loc.y);
  }
}

Below is some particularly beautiful outputs from this code; all of it is generated simply by modifying the constants at the top of the file. TWIST is the amount that the direction is offset; a TWIST of 0 means we move towards the selected vertex head-on. STEP_RATIO is the proportion of the total distance to that vertex that we move. ALLOW_SAME_VERT and ALLOW_NEIGHBOR_VERT are pretty self-explanatory, controlling whether or not we can select the same vert or neighboring verts in the next iteration respectively.

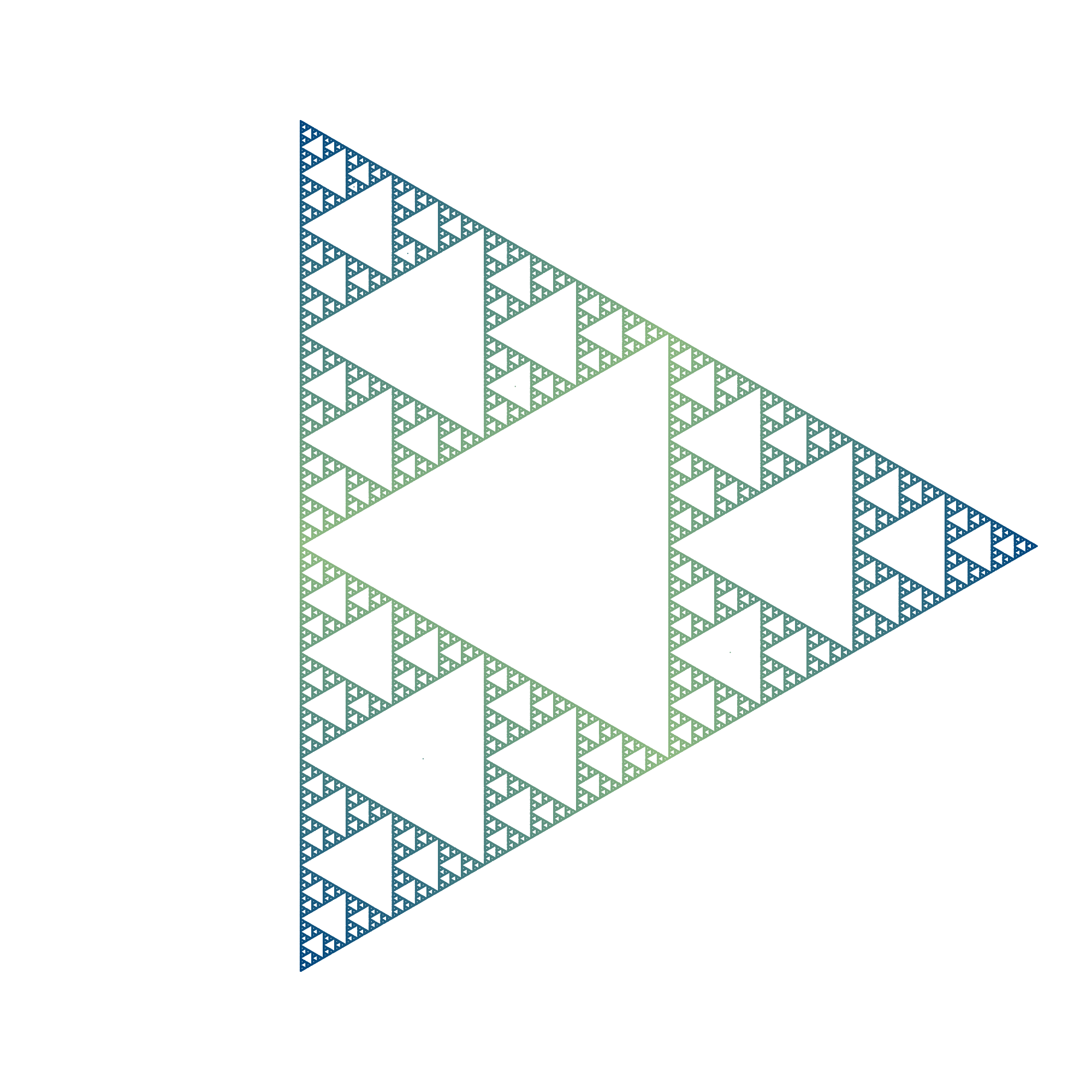
TWIST = 0.0, STEP_RATIO = 1/2, ALLOW_SAME_VERT = true, ALLOW_NEIGHBOR_VERT = true. This is the Sierpiński triangle that we constructed at the beginning; it’s not a coincidence that we got this pattern!

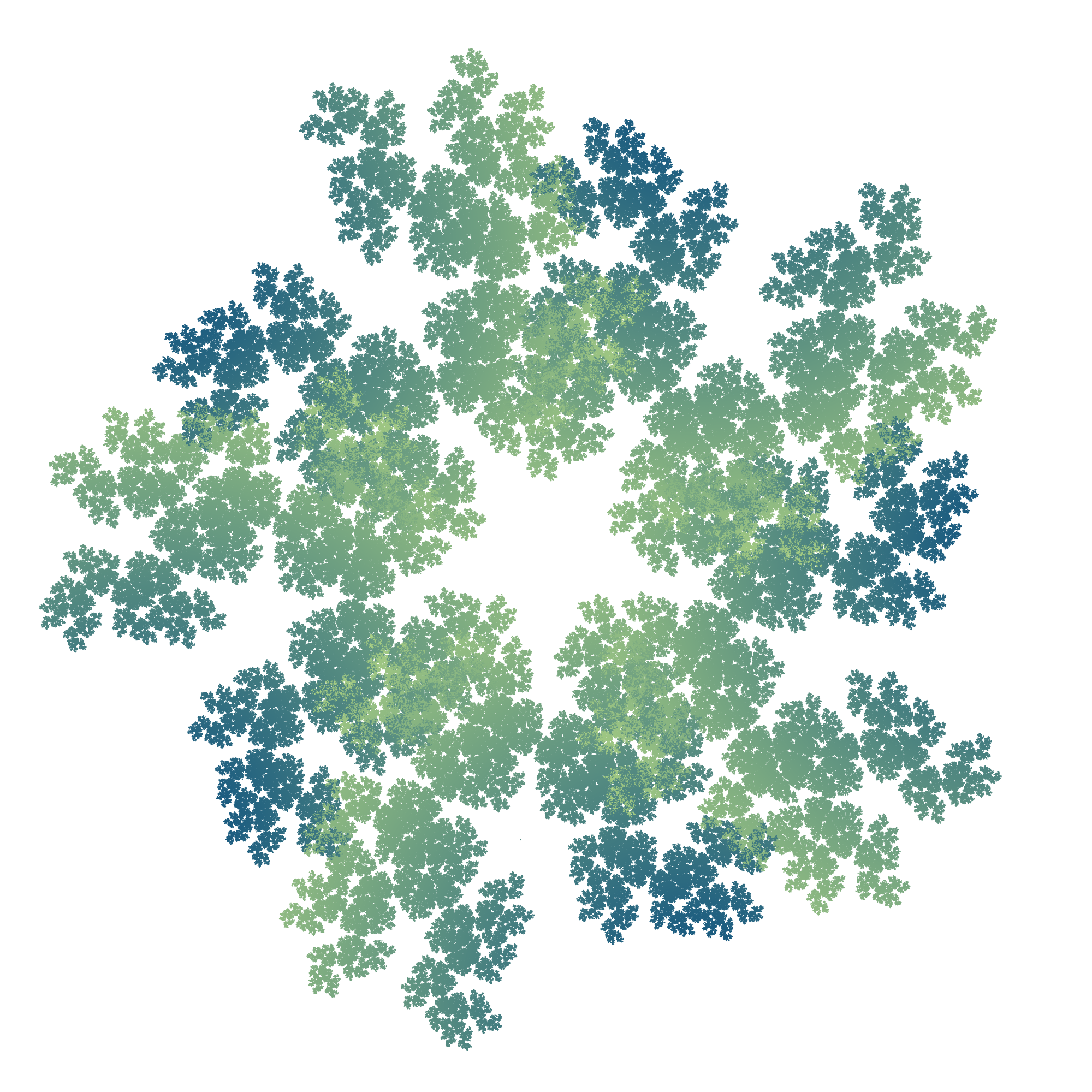
TWIST = 0.4, STEP_RATIO = 3/5, ALLOW_SAME_VERT = true, ALLOW_NEIGHBOR_VERT = false.

TWIST = 0.0, STEP_RATIO = 3/5, ALLOW_SAME_VERT = false, ALLOW_NEIGHBOR_VERT = true.

TWIST = -0.3, STEP_RATIO = 3/5, ALLOW_SAME_VERT = false, ALLOW_NEIGHBOR_VERT = false.

TWIST = 0, STEP_RATIO = 11/20, ALLOW_SAME_VERT = true, ALLOW_NEIGHBOR_VERT = true.

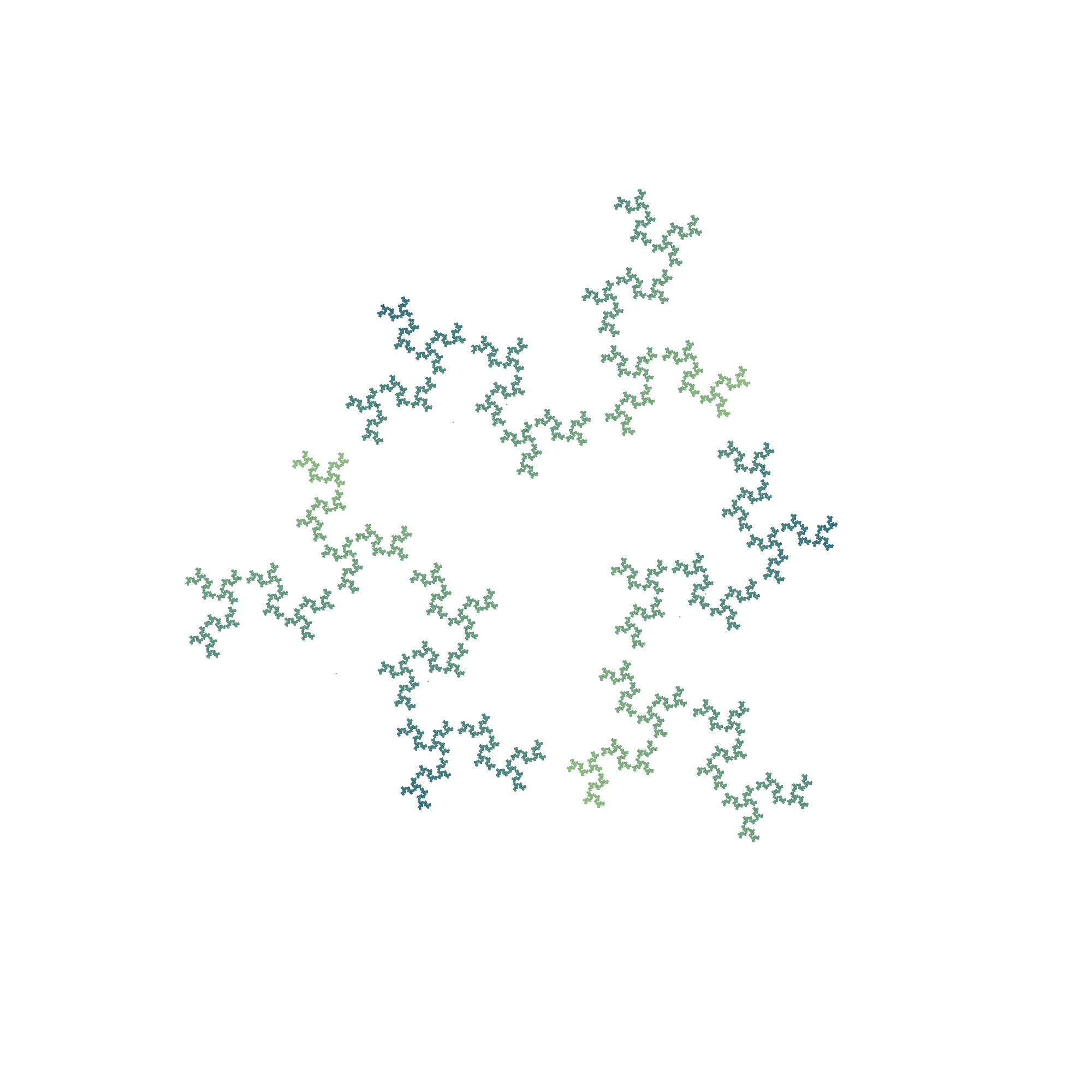
TWIST = 0.5, STEP_RATIO = 1/2, ALLOW_SAME_VERT = false, ALLOW_NEIGHBOR_VERT = true.

TWIST = 0.2, STEP_RATIO = 3/5, ALLOW_SAME_VERT = true, ALLOW_NEIGHBOR_VERT = true.

The variability in size, detail, shape, and clarity that can be acheived by just tweaking a few variables is very beautiful. Just a simple idea of moving a point between a few vertices randomly is enough to generate infinite levels of detail; it’s surprising how randomness can contribute so readily to something so orderly and structured like a fractal.